Rendezvous in orbital dynamics is a pretty interesting problem. You’ve got multiple frames of references, different orbits, solar radiation effects/pressures and more - all complexity that exists without even factoring in thinking about relative motion for any purpose. We’ve been doing more of them lately, Hayabusa2, DART (Double Asteroid Redirection Test!) and the MEV are some of my favorites.

Purpose for rendezvous then clearly comes in different shapes, but the one I’ve been playing around with lately has been for RPO, or Rendezvous and Proximity Operations.

The underlying economic reasons (outside of it just being a cool thing to do) boils down to the cost benefit analysis of decommisioning a satellite after some failure or sending up another one (or paying another org to do so) to perform some corrective measures. MEV is a good example of this, with MEV-1 having serviced an Intelsat satellite to extend its lifespan.

There are other use cases (like spying or performing offensive actions against a satellite) but really if you can match velocities in orbit to fix a satellite you can do the same to break one.

There’s a number of ways to model the dynamics of RPO, which start ballooning in complexity depending on what you want to do. Here’s an example of a complex maneuver I modeled the other day, which includes a v-bar hop and a teardrop maneuver, commonly used for reconnaisance or more “interesting” missions.

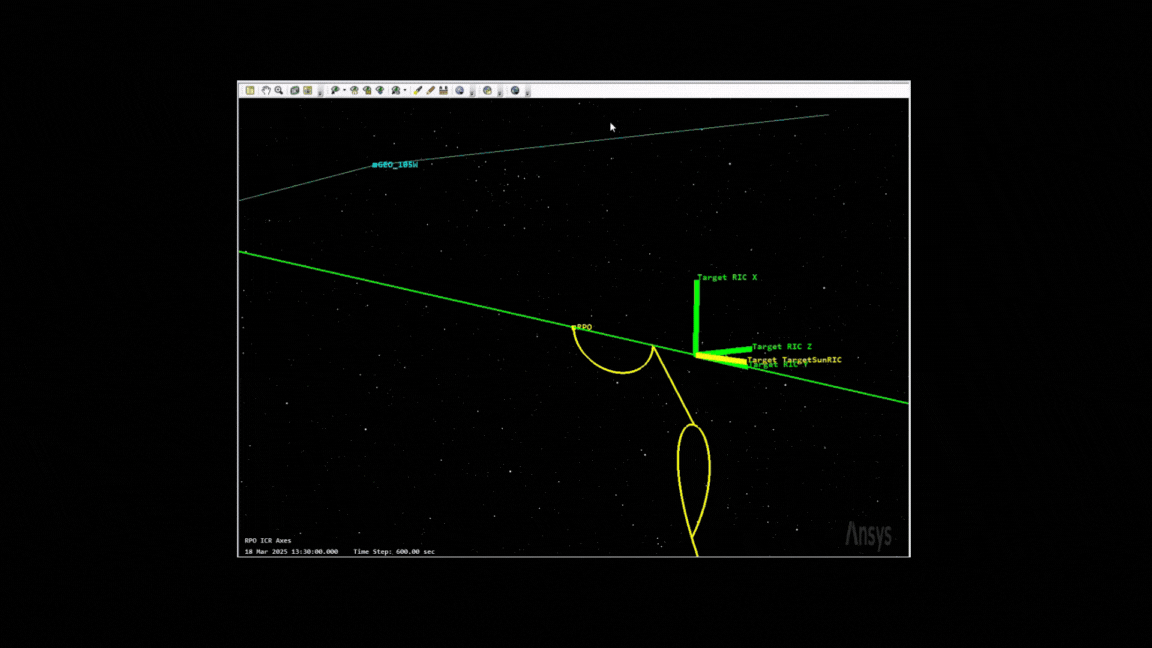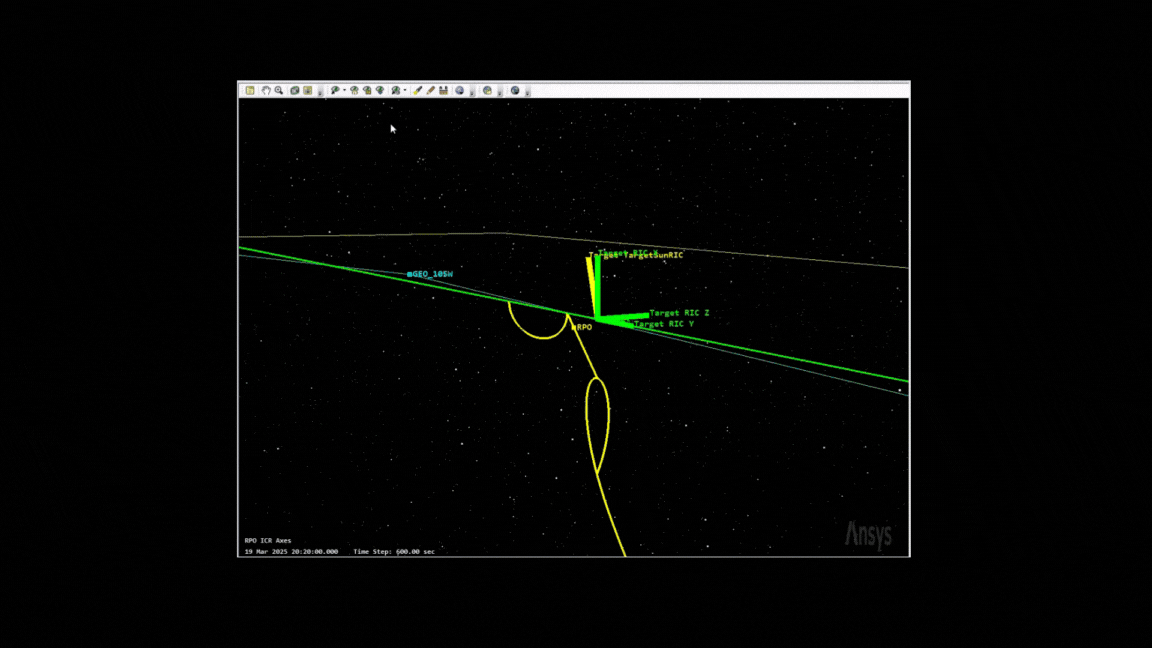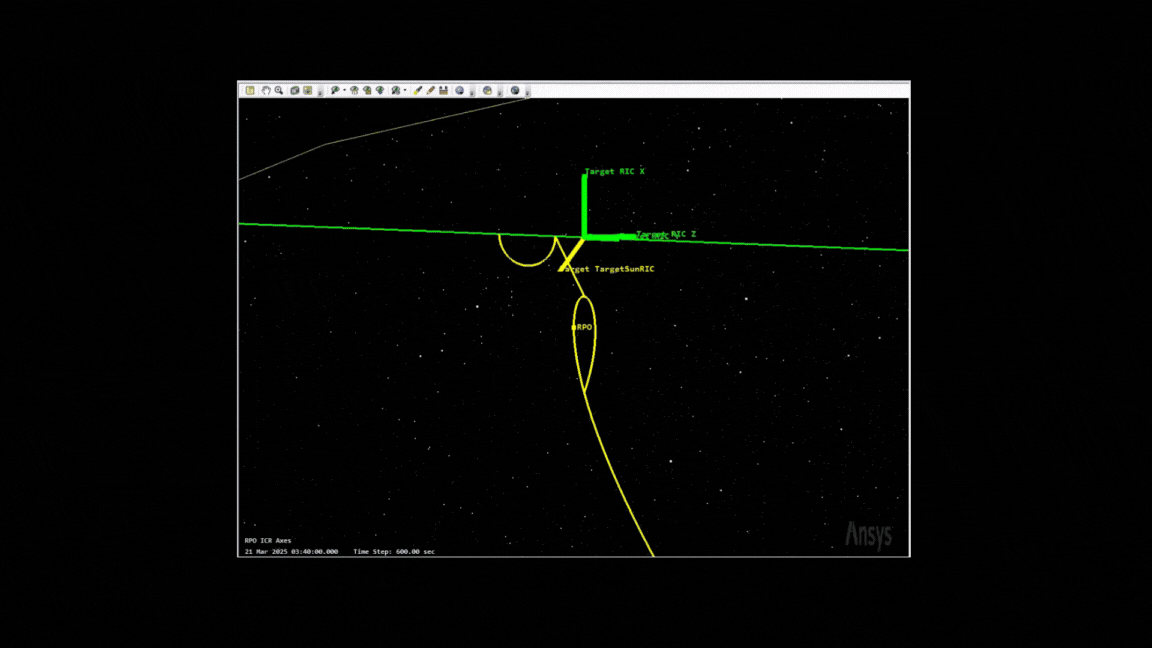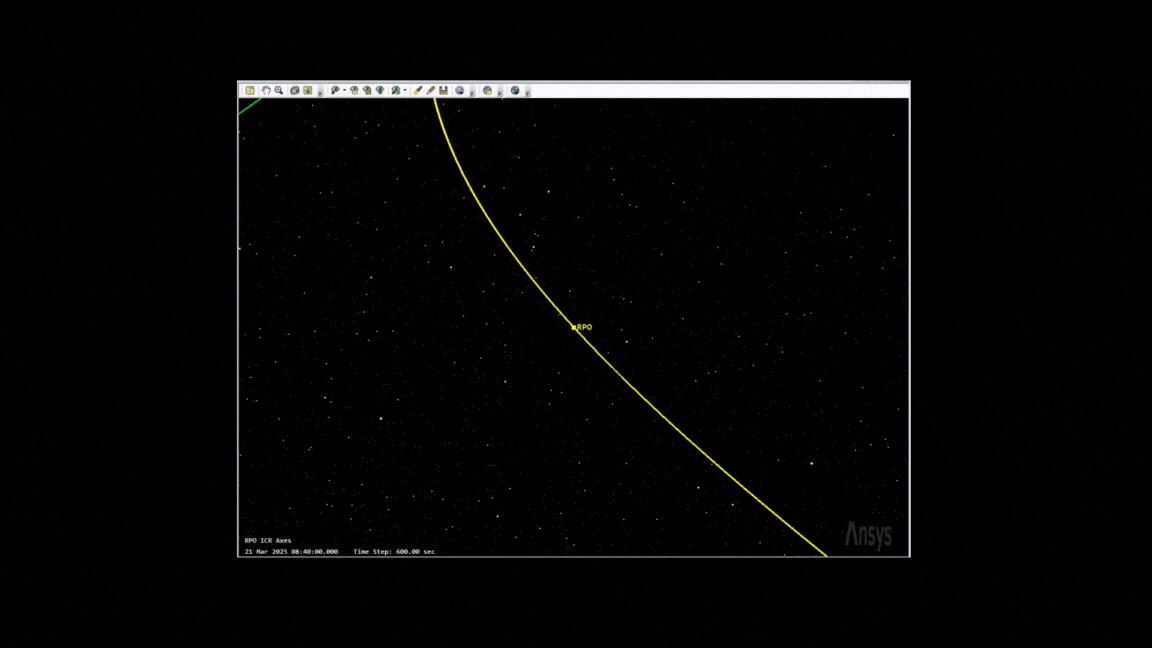
Outside of the intent, I think teardrop rendezvous are the most romantic.

An approximate model that gets you fairly far is the Clohessy-Wiltshire equations, which allows for modeling the chaser’s motion in a target-centered frame. This is a good link if you’re curious about the derivation.

Below is some julia code walking through propagating them for a given time t, with the output being a 1x6 vector of: $$\left[ x, y, z, \dot{x}, \dot{y}, \dot{z} \right]$$ .

function PropagateCW(
    X0::SVector{6, Float64},
    t::Float64,
    ω::Float64,
    )

    ϕ = zeros(6, 6)
    n = ω
    τ = n * t

    # Position-to-position (Φ_rr)
    ϕ[1,1] = 4 - 3*cos(τ)
    ϕ[2,1] = 6*(sin(τ) - τ)
    ϕ[2,2] = 1
    ϕ[3,3] = cos(τ)

    # Position-to-velocity (Φ_rv)
    ϕ[1,4] = (1/n)*sin(τ)
    ϕ[1,5] = (2/n)*(1 - cos(τ))
    ϕ[2,4] = (2/n)*(cos(τ) - 1)
    ϕ[2,5] = (1/n)*(4*sin(τ) - 3*τ)
    ϕ[3,6] = (1/n)*sin(τ)

    # Velocity-to-position (Φ_vr)
    ϕ[4,1] = 3*n*sin(τ)
    ϕ[5,1] = 6*n*(cos(τ) - 1)
    ϕ[6,3] = -n*sin(τ)

    # Velocity-to-velocity (Φ_vv)
    ϕ[4,4] = cos(τ)
    ϕ[4,5] = 2*sin(τ)
    ϕ[5,4] = -2*sin(τ)
    ϕ[5,5] = 4*cos(τ) - 3
    ϕ[6,6] = cos(τ)

    X = SVector{6}(ϕ * X0)
    return X
end

One of the biggest limits of the CW equations is that it’s only valid for circular orbits (for the target) and is only valid for natural motion circumnavigation - where the chasing satellite (once in position) needs minimal thrust to maintain position. The teardrop maneuver from the gif above is an example of forced-motion navigation - where constant delta-Vs allow you to keep a position for a limited period of time. Another favorite of mine is the Walking Safety Ellipse.

# Walking Safety Ellipse (WSE) function using HCW functions
function WSE(x_max::Float64, y_max::Float64, ω::Float64, x_c::Float64, xdot_c::Float64)
    t = range(0.0, stop=1000000.0, length=10000)
    x = [(2 * x_max * cos(ω * ti)) + (xdot_c * (ω * ti - pi / 2)) / ω + x_c for ti in t]
    y = [y_max * cos(ω * ti) for ti in t]
    z = [(x_max * sin(ω * ti)) - (2 * xdot_c) / (3 * ω) for ti in t]

    p = plot3d(x, y, z, label="WSE", color=:red, xlabel="X (km)", ylabel="Y (km)", zlabel="Z (km)")
    savefig(p, "WSE.png")

    return p
end

Which given some target $\dot{x_c}$ and $x_c$ - the radial velocity and initial radial offset, give you a pretty graph like this, tracing a chaser following a target (but at a safe designed distance of $x_{max}$ and $y_{max}$).

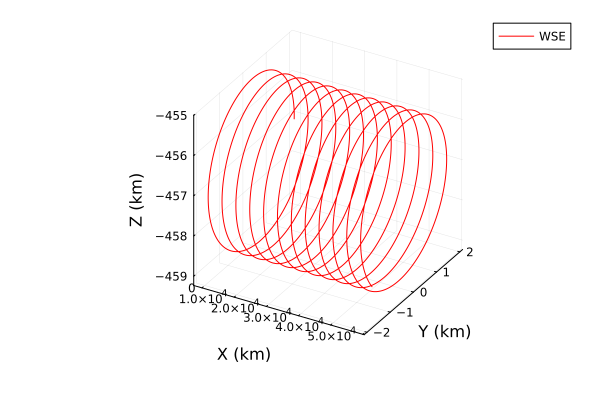
Another romantic rendezvous maneuver.